I enjoy making things—especially software! 🧑‍💻

For me, coding is a heady combination of 🖋️ writing and 🧩 puzzle solving and ❤️ care. And sometimes the software ends up being useful, too. 😄

Here are some of the projects I've worked on.

Theanets📖

theanets is a neural network toolkit for Python that uses Theano for the heavy lifting. Thanks to Theano, your models will transparently run on a GPU.

The toolkit makes it easy to create a wide variety of machine learning models, including linear dense and sparse autoencoders (e.g., PCA and ICA), denoising autoencoders, linear and nonlinear regression, regularized regression (e.g., lasso or elastic net), linear and nonlinear classifiers, and recurrent autoencoders and classifiers, including models using LSTM cells or Clockwork RNN layers.

Models can be constructed using different activation functions (e.g., linear, rectified linear, batch normalization, etc.) and different numbers of layers (e.g., deep models). It is also easy to add different regularizers to each of the models at optimization time—in fact, regularization is often what differentiates two otherwise very similar models (e.g., PCA and ICA).

import theanets, numpy as np

def sample(n): return np.random.randn(n, 10)

# create an autoencoder model.
ae = theanets.Autoencoder([10, 2, 10])

# train it with a sparsity regularizer.
ae.train(sample(1000), sample(100),
         algo='rmsprop', hidden_l1=0.1)

# continue training without the regularizer.
ae.train(sample(1000), sample(100),
         algo='nag', momentum=0.9)

# use the trained model.
ae.predict(sample(10))

Downhill📖

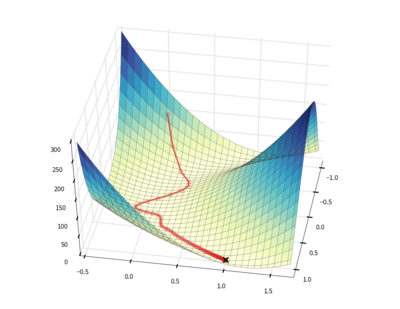
downhill is a collection of stochastic gradient optimization routines for loss functions defined using Theano.

The package implements vanilla stochastic gradient descent (SGD), resilient backpropagation, RMSProp, ADADELTA, Equilibrated SGD, and Adam. All optimization algorithms can be combined with traditional and Nesterov (PDF) momentum.

import climate, downhill, theano, numpy as np
import theano.tensor as TT

climate.enable_default_logging()

def rand(*s): return np.random.randn(*s).astype('f')

# Set up a matrix factorization problem to optimize.
A, B, K = 20, 5, 3
u = theano.shared(rand(A, K), name='u')
v = theano.shared(rand(K, B), name='v')
e = TT.sqr(TT.matrix() - TT.dot(u, v))

# Create a noisy low-rank matrix to factor.
z = np.clip(rand(A, K) - 0.1, 0, 10)
y = np.dot(z, rand(K, B)) + rand(A, B)

downhill.minimize(
    # loss = |x - uv|_2 + |u|_1 + |v|_2
    loss=e.mean() + abs(u).mean() + (v * v).mean(),
    train=[y], batch_size=A, max_gradient_norm=1,
    learning_rate=0.1)

print('Sparse Coefficients:', u.get_value())
print('Basis:', v.get_value())

Pagoda

Combines the ODE physics simulator with some OpenGL tools for visualization, and a simple grammar for defining articulated bodies.

import click, pagoda, pagoda.viewer, numpy as np

# Implement a custom world reset that randomly repositions things.
class World(pagoda.physics.World):
    def reset(self):
        for b in self.bodies:
            b.position = np.array([0, 0, 10]) + 3 * rng.randn(3)
            b.quaternion = pagoda.physics.make_quaternion(
                np.pi * np.random.rand(), 0, 1, 1)

# Helper for generating gamma-distributed random values.
def gamma(n, k=0.1, size=1):
    return np.clip(np.random.gamma(n, k, size=size), 0.5, 1000)

w = World()

# Create 100 bodies in the world -- random shape, size, and color.
for _ in range(100):
    shape, kwargs = sorted(dict(
        box=dict(lengths=gamma(8, size=3)),
        capsule=dict(radius=gamma(3), length=gamma(10)),
        cylinder=dict(radius=gamma(2), length=gamma(10)),
        sphere=dict(radius=gamma(2)),
    ).items())[np.random.randint(4)]

    body = w.create_body(shape, **kwargs)
    body.color = tuple(np.random.uniform(0, 1, size=3)) + (0.9, )

# Run the simulation!
w.reset()
pagoda.viewer.Viewer(w).run()

Others

py-c3d
A small set of utilities—at this point consisting of a file reader and writer, and a simple OpenGL visualization tool—for dealing with motion capture data files in the C3D binary format.
py-depparse
A Python library and command-line tool for non-projective dependency parsing of natural language text.
kohonen
A collection of several vector quantizers, including self-organizing (Kohonen) map, neural gas, and growing neural gas.
py-rbm
Single-module implementation of Several types of Restricted Boltzmann Machines.
py-trm
A Python wrapper for the Gnuspeech Tube Resonance Model, a vocal synthesizer.